What is ELO Model Actually

Background

When we talk about the forecasting in sports, ELO model is the most common thing. However, what is ELO actually? Based on Wikipedia, the Elo rating system is a method for calculating the relative skill levels of players such as chess.

ELO formula

If team A plays against team B, the probability of win for team A is like the equation below. If the ELO score of team A and B are the same, then the probability of win is 50%, which make sense. \(P_{Awin}=\frac{1}{1+10^{\left(ELO_{B}-ELO_{A}\right) / 400}}\)

ELO vs Logestic Regression

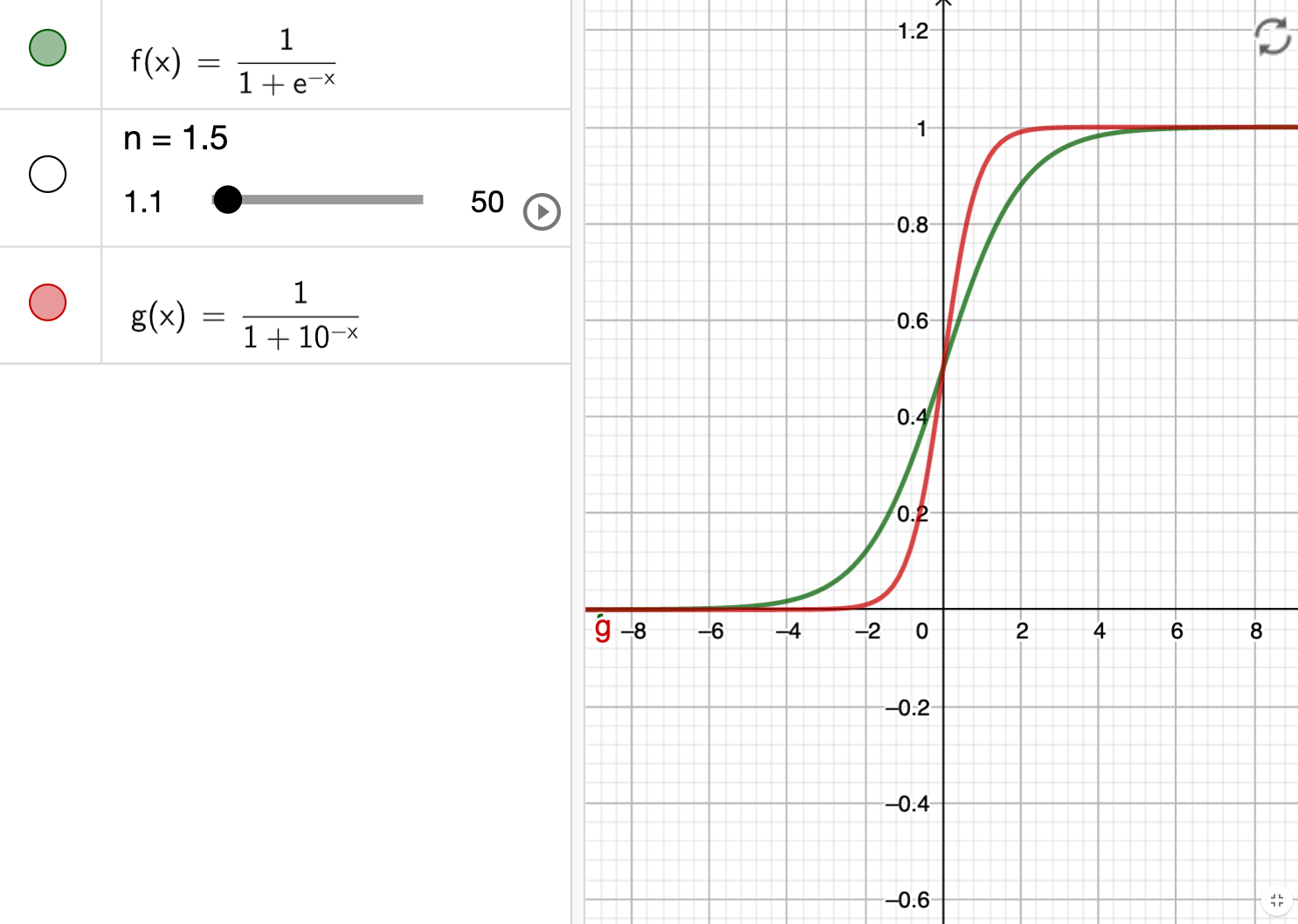
The formular is very simialr with logistic function (sigmoid function) with different base. \(f(x)=\frac{1}{1+e^{-x}}\)

The plot shows the clear different between two equations, which brings us the next questions: why the base is 10 and why the score need to be divided by 400?

K factor

The way of updating the elo scores is shown as following. K is the factor that we need to give in advance. Initially, k is a constant number in different games (e.g. 40 or 32). When k is 40, that means maximum of elo score of each game is 40. \(\text {elo}_{new}=\mathrm{elo}_{old}+k\left(outcome-\operatorname{P}_{win}\right)\)

One of solution is to use a dynamic K based on the number of matches in tennis. read the artical here

Dynamic K based on Margin

One of the examples of using dynamic k based on margin is like this in NBA. I am not interested in whethere it works or not. The question is where those numbers come from in the equation. I’ve no idea so far. \(\mathrm{K}=20 \frac{\left(\mathrm{Margin}_{\text {winner }}+3\right)^{0.8}}{7.5+0.006\left(\text { elo_difference }_{\text {winner }}\right)}\)

Home advantage

Home advanage is a positive factor for all sport games when calculating the probabilty of winning. i.e. The home team can have addtional elo scores. Again, you can setup a constant number first intuitively. Then, you can optimize it as a parameter.

Year-to-Year Carry-Over

For yearly sports game, the common issue is that how to handle seasons. The straightforward way is to give a decay. The example: \(Elo_{this_season}=(0.75)*Elo_{last_eason}+(0.25)*1505\)

*1505 is the base elo score

Future work

• For team sports, player-level data is not included. If the key player get injured, the ELO rating system get the info slowly.
• Definitely ELO is not the only solution, lots of other probabilitic and ML models can work in some scinarios.